Sortieralgorithmen verstehen! Am Beispiel von Insertion-Sort in Java.

Keylearnings:

• Was sind Sortieralgorithmen?
• Die Eigenschaften von Sortieralgorithmen?
• Der Insertion-Sort Algorithmus.
• Die Komplexität von Insertion-Sort?

Ein Griff und du hast es gefunden?

Oder.

Ein Griff und die Suche kann beginnen?

Den Unterschied macht die Ordnung!

So ist es auch wenn wir in einer Datenstruktur nach einem Datensatz suchen.

In einem sortierten Datenbestand kann eine Abfrage bedeutend schneller bearbeitet werden.

Aber wie können wir sicherstellen, dass in unserer Datenstruktur Ordnung herrscht?

Hier haben wir zwei Möglichkeiten:

1. Wir sorgen beim Einfügen eines Datensatz dafür, dass der Datenbestand sortiert bleibt.
2. Wir räumen unsere Datenstruktur regelmäßig auf.

Welche Methode die bessere ist, hängt davon ab, ob wir überwiegend lesend oder schreibend auf unseren Datenbestand zugreifen müssen.

Die erste Möglichkeit führt zu einem höheren Aufwand beim Einfügen eines Datensatzes.

Bei Möglichkeit zwei entsteht, durch das regelmäßige Sortieren, ein höherer Pflegeaufwand, dafür können wir aber sehr einfach Datensätze in den Datenbestand einfügen.

In diesem Artikel beschäftigen wir uns mit Möglichkeit zwei und schauen uns an, wie wir eine Datenstruktur sortieren können.

Genau DAS ist nämlich die Aufgabe von Sortieralgorithmen. Ein konkretes Beispiel für einen Sortieralgorithmus ist der Insertion Sort, den wir uns im Detail ansehen wollen.

Was ist ein Sortieralgorithmus?

Für einen Sortieralgorithmus benötigen wir zwei Dinge.

1. Eine Menge, die wir ordnen wollen. Hierbei ist die ungeordnete Menge die Eingabe und die geordnete Menge die Ausgabe des Algorithmus.
2. Ein Verfahren mit dem wir die Menge effizient sortieren können.

Auch müssen wir uns überlegen was es denn überhaupt bedeutet, dass ein Element a vor einem anderen Element b liegt. In Java können wir das sehr komfortabel mit Hilfe der Comparator Schnittstelle machen.

Der Einfachheit wegen beginnen wir mit einem Array von Integer-werten, die wir aufsteigend sortieren wollen.

Sortieralgorithmen sind  gut erforscht und es wurden effiziente Verfahren entwickelt. Berühmt geworden sind insbesondere folgende Sortieralgorithmen:

• Selection-Sort
• Bubble-Sort
• Insertion-Sort
• Merge-Sort
• Quick-Sort

Und wieder einmal haben wir die Qual der Wahl.

Anstatt uns jeden Sortieralgorithmus einzeln vorzuknöpfen, wollen wir uns die entscheidenden Merkmale am Beispiel des Insertion-Sort Algorithmus ansehen.

Eigenschaften eines Sortieralgorithmus

Was macht einen guten Sortieralgorithmus aus?

Zeit- und Speicherkomplexität!

Wie immer soll unser Algorithmus eine möglichst geringe Zeit- und Speicherkomplexität aufweisen.

Insbesondere möchten wir, dass bei steigendem Datenvolumen die Komplexität so gering wie möglich ansteigt. Diese Eigenschaft, lässt sich mit Hilfe der O Notation messen.

Leider auch wie (fast) immer sind Zeit- und Speicherkomplexität gegenläufig.

Häufig werden Hilfsdatenstrukturen verwendet, welche zwar die Speicherkomplexität erhöhen, dafür aber die Zeitkomplexität verbessern.

Um die Zeitkomplexität zu verringern müssen wir dafür sorgen, dass  so wenige Tauschoperationen wie möglich stattfinden womit wir auch gleich bei der nächsten Eigenschaft sind.

Die Anpassbarkeit!

Im Idealfall sollte eine bereits sortierte Liste schneller sortiert sein (in 0 Schritten), als eine Liste, in der das totale Chaos herrscht.

Leider fehlt vielen Sortieralgorithmen der Blick für das Ganze, sodass die Verarbeitung einer bereits sortierten Liste genauso viel Zeit in Anspruch nimmt wie die einer unsortierten Liste.

Da wir bei der O Notation immer das Worst-Case Szenario betrachten, führt die Eigenschaft der Anpassbarkeit dazu, dass Algorithmen, die in der Theorie besser sein müssten, in der Praxis eine höhere Laufzeit haben.

Ein Sortieralgorithmus, der die Eigenschaft Anpassbarkeit unterstützt ist der Insertion Sort Algorithmus, den wir uns im folgenden detailiert ansehen wollen.

Der Insertion-Sort Algorithmus

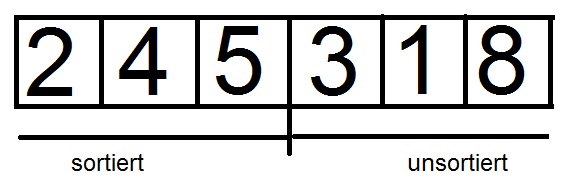
Im Insertion-Sort Algorithmus gehen wir davon aus, dass die zu ordnende Liste aus zwei Teilen besteht. Einem geordneten Teil und einem ungeordneten Teil.

Bei einer vollkommen unsortierten Liste besteht der geordnete Teil zu Beginn aus einem einzelnen Element. Eine Liste die nur aus einem einzigen Element besteht ist nämlich IMMER sortiert.

Kompliziert? Okay, ich zeigs dir!

Schauen wir uns folgendes Array an:

Bei den ersten drei Elementen handelt es sich um eine sortierte Liste, daher beginnt der Insertion Sort Algorithmus seine Arbeit erst ab Position Vier.

Je besser die Liste sortiert ist desto weniger Schritte sind also notwendig. Hieran erkennen wir die Anpassbarkeits-Eigenschaft des Insertion Sort Algorithmus.

Ziel beim Insertion-Sort ist es den sortierten Teil der Liste schrittweise zu vergrößern.

In unserem Fall bedeutet dies, dass wir das vierte Element, also den Wert 3 an die richtige Stelle einsortieren müssen.

Dazu vergleichen wir das Element an dritter Position, also den Wert 5 mit dem Wert 3 an Position vier. Da 5 größer als 3 ist vertauschen wir die Elemente und wir erhalten.

Als nächstes vergleichen wir Position drei (Wert 3) mit Position zwei (Wert 4). Da 4 größer als 3 ist müssen wir die Elemente vertauschen.

Nach diesem Schritt ist der sortierte Anteil der Liste um ein Element gewachsen.

Jetzt verfahren wir analog mit dem ersten Element der unsortierten Liste (Position 5). D.h. wir vergleichen Position vier und fünf miteinander und stellen fest, dass 5 größer 1 gilt und vertauschen die Elemente miteinander.

Als nächstes wird Position drei und vier miteinander verglichen und wieder stellen wir fest, dass diese Elemente miteinander vertauscht werden müssen und wir erhalten.

Auf diese Weise verfahren wir solange bis der Wert 1 bis ganz nach vorne gewandert ist und wir schließlich eine sortierte Liste erhalten haben.

Gut! Kümmern wir uns als nächstes um die Implementierung!

Die Implementierung von Insertion-Sort

Die Implementierung des Insertion-Sort Algorithmus teilt sich in zwei Schritte auf.

Zunächst muss das erste Element der unsortierten Liste gefunden werden und anschließend durch Tauschoperationen an die richtige Position in dem sortierten Teil der Liste gebracht werden.

Das machen wir mit zwei ineinander verschachtelten Schleifen.

Die erste Schleife durchläuft das gesamte Array vom ersten bis zum letzten Element. In der zweiten Schleife durchlaufen wir den sortierten Teil der Liste rückwärts und bringen das einzusortierende Element durch Vertauschungen von Nachbarelementen an die korrekte Position.

1: public static void insertionSort(int[] liste){
2:	int temp = 0;
3:	int j = 0;
4:	for(int i = 1;i < liste.length;i++){ 
5:           j = i; 
6:           while((j>0)&&(liste[j-1]>liste[j])){
7:		temp = liste[j-1];
8:		liste[j-1] = liste[j];
9:		liste[j] = temp;
10:		j--;
11:	    }
12:	}
13:}

Wir brechen die while Schleife in Zeile 6 ab, sobald wir entweder den Anfang der Liste erreicht haben (j>0) oder das einzusortierende Element die richtige Position im sortierten Teil der Liste erreicht hat (liste[j-1]>liste[j]).

In jedem Schleifendurchlauf werden Nachbarelemente vertauscht wobei es sich bei dem rechten Element um das einzusortierende (das erste Element der unsortierten Liste) Element handelt. Um die Vertauschung durchführen zu können benötigen wir eine Hilfsvariable temp.

Dieser Vorgang wird solange wiederholt bis das einzusortierende Element an die richtige Position im sortierten Teil der Liste gewandert ist.

Im folgenden Video wiederhole ich die einzelnen Schritte, die beim Insertion-Sort Algorithmus durchgeführt werden:

Okay, machen wir einen Probelauf mit dem Array aus dem Beispiel von oben.

1: int test[] = {2,4,5,3,1,8};
2: insertionSort(test);
3: for(int i = 0;i<test.length;i++){
4:	System.out.print(test[i]+" ");
5: }

Nicht sehr spektakulär!

In Zeile Eins initialisieren wir ein Test-Array, das wir in Zeile 2 als Argument an die insertionSort Funktion übergeben.

Anschließend geben wir das sortierte Array in einer for Schleife (Zeile 3-5) aus.

Die Bildschirmausgabe sieht wie folgt aus:

1 2 3 4 5 8

Sauber! Schauen wir uns die Zeitkomplexität an.

Die Zeitkomplexität des Insertion Sort Algorithmus

Bei der O Notation betrachten wir den schlechtesten Fall.

Die for Schleife in Zeile vier durchläuft das gesamte Array, ab der zweiten Stelle. D.h. bei einem Array der Länge N finden N-1 Schleifendurchläufe statt.

In der while Schleife in Zeile 6 kommt die Anpassbarkeit des Insertion-Sort Algorithmus zum tragen. Bei einer bereits sortierten Liste wird die while Schleife Null mal durchlaufen.

Der schlechteste Fall tritt auf, wenn wir eine absteigend sortierte Liste in eine aufsteigend sortierte Liste umwandeln wollen.

Überlegen wir uns wie oft der while Schleifen-Inhalt im folgenden Beispiel ausgeführt werden muss.

Da es sich hierbei um ein absteigend sortiertes Array handelt, besteht die sortierte Liste am Anfang nur aus dem Element mit dem Wert 8.

Die unsortierte Liste beginnt mit dem Element, das den Wert 5 enthält, um dieses an die richtige Position in der sortierten Liste zu bringen ist eine Vertauschung notwendig, d.h. die while Schleife wird genau einmal durchlaufen.

Nach diesem Schritt hat die Liste folgende Gestalt:

Unser Plan ist aufgegangen und der sortierte Teil der Liste hat sich um ein Element vergrößert. Der unsortierte Teil beginnt mit dem Element, das den Wert 4 enthält. Diesmal benötigen wir zwei while Schleifendurchläufe, also auch zwei Tauschoperationen um den Wert 4 an die richtige Position in der sortierten Liste zu bringen.

Jetzt hat unser Array folgende Gestalt:

Und wieder ist der sortierte Teil um ein Element gewachsen. Nun muss das Element mit dem Wert 3 einsortiert werden.

Hierfür benötigen wir drei while Schleifen durchläufe. Oder mit anderen Worten drei Tauschoperationen.

Langsam aber sicher ist ein Bildungsgesetz zu erkennen. Als nächstes müssen wir den Wert 2 in die richtige Position bringen wofür wir vier Tauschoperationen benötigen.

Jetzt haben wir es fast geschafft. Wir müssen noch das letzte Element mit dem Wert 1 nach vorne wandern lassen. Wofür wir fünf weitere while Schleifendurchläufe benötigen.

Lass uns den Taschenrechner anschmeißen und die Gesamtanzahl der Tauschoperationen bzw. der while Schleifendurchläufe aufaddieren.

Wir erhalten:

Anzahl Tauschoperationen = 5 + 4 +3 + 2 + 1 = 15.

Um ein Array mit sechs Elementen zu sortieren, werden also im schlechtesten Fall 15 Tauschoperationen benötigt.

Mit Hilfe eines scharfen Blickes stellen wir die Vermutung auf, dass für ein Array mit n Elementen im schlechtesten Fall

Anzahl Tauschoperationen = (n-1)+(n-2)…..+2+1

gilt. Diese Vermutung kann mithilfe eines Induktionsbeweises bestätigt werden.

Mit Hilfe der Gaußformel können wir obigen Ausdruck noch vereinfachen und wir erhalten.

Anzahl Tauschoperationen = n(n-1)/2 .

Und da bei der O Notation nur der Term vom höchsten Grad zu beachten ist und außerdem Konstanten keine Rolle spielen erhalten wir O(N²).

Der Insertion-Sort Algorithmus ist also von quadratischer Komplexität.

Fazit: Auch wenn die meisten Programmiersprachen Sortieralgorithmen von Haus aus mitbringen, gehört die Kenntnis von Suchalgorithmen zur Allgemeinbildung eines Informatikers. Der Insertion-Sort ist ein klassisches Beispiel für einen Suchalgorithmus.

Ich freue mich auf deine Fragen im Kommentarbereich.

Hat dir der Artikel gefallen? Dann folge uns am besten gleich auf Facebook!